今日はカンガルー君が、
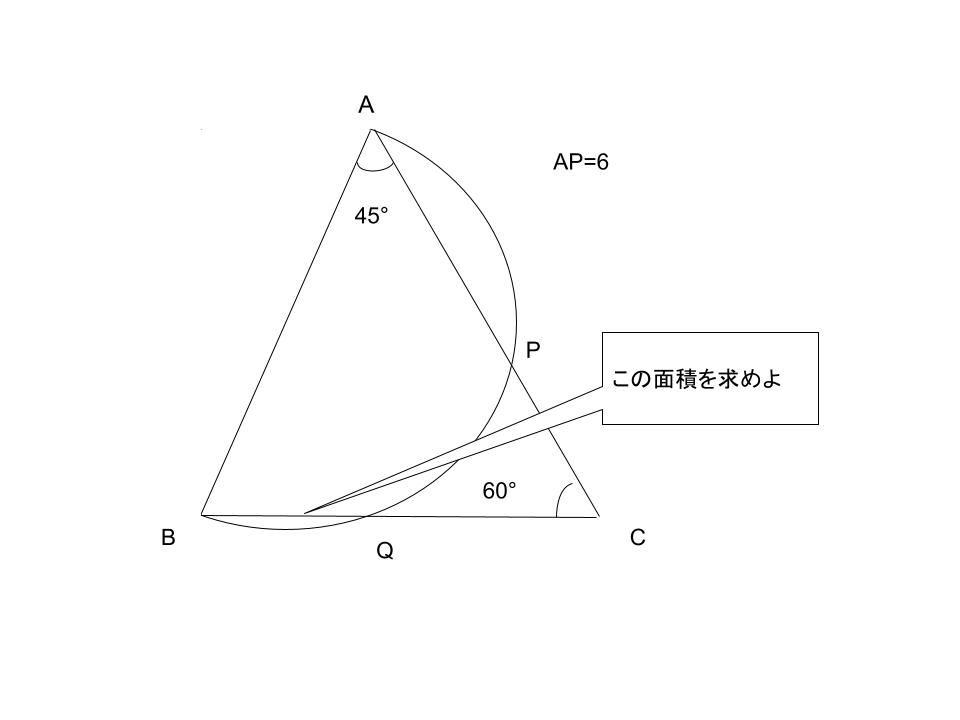
三角形ABCとABを直線とする半円とが2点P,Qで交わっています。
辺ACのうち、APの長さは6cmです。
この面積の求め方を教えてやるから、
家まで来いと言われて、
カンガルー君の家まで来ました。

こんにちはカンガルー君。
今日は図形の勉強かい?

これは中学入試の問題や。
こんな問題なんてことないやろ?

まったくわからないよ。
あんなに狭いところの面積なんか、
わかるわけないじゃないか。

中学生入試やで、
小学生が解く問題や。

そんなに優秀な小学生が、
この世にいるのですか?

まあ、説明したるから、
聞いていきなはれ。

よろしくお願いいたします。

まずはBPの長さはいくつや?

わかりません。

ホンマあほやな。
半円の端と端で、
円のどの点を結んでも、
角度が90°になるんや。

へー

つまりは、三角形ABPは、
二等辺三角形や。
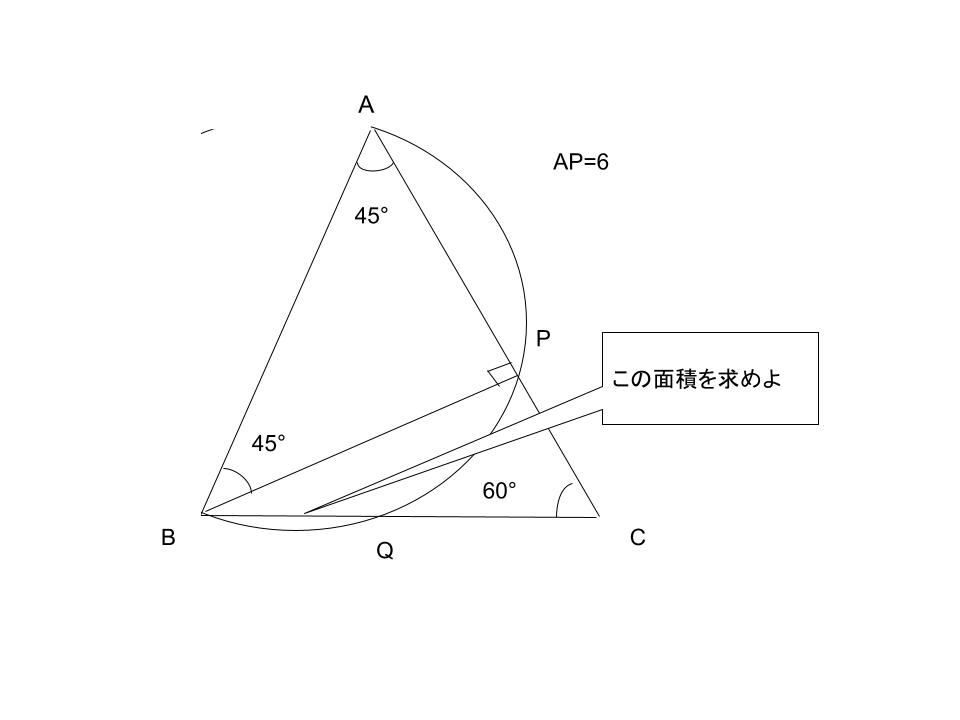

つまりは、BPは6cmということだね。

やるやないかい。
次は辺ABの真ん中に、
点Oを付けて、
三角形AOPを作るんや。
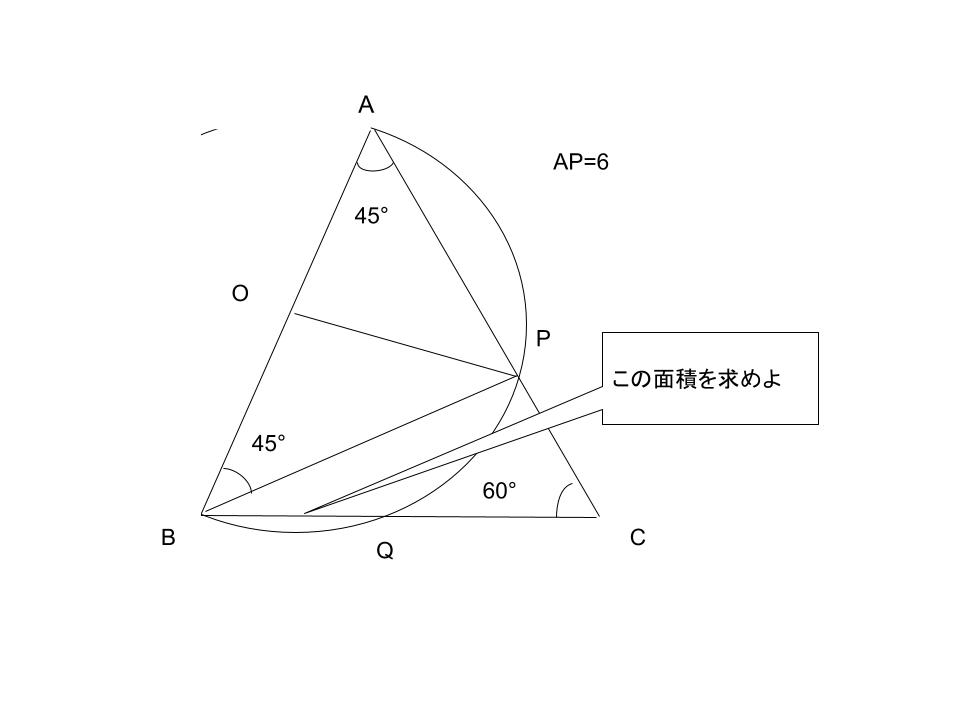

直角二等辺三角形だね。

この三角形AOPの、
面積を求めるねん。

直角二等辺三角形だから、
二つ重ねて、正方形にして、
対角線x対角線÷2÷2だね。

やるやないかい。
ヒポクラテスの三日月を
忘れてへんな。

えへへ。
答えは9㎠だね。

ホンマにスッキリやで。

じゃあ、今日はこのへんで…

ちょまてや。
誰が三角形の面積で終われんねん。

冗談ですよ。

三角形AOPの面積が9㎠。
AOとOPは底辺と高さや、
つまりは?

三角形の面積の出し方で、
底辺×高さ÷2だから、
AO×OP÷2=9

AOとOPは共に半径やから、
半径×半径が18いうことや。

すごいよカンガルー君。
半径はわからないままでも、
半径×半径はわかったんだね。

これが算数のおもろいところやねん。

つまり、この半円の面積は、
12×3.14÷2だから、
28.26だ!

さすがはまもるや。
教えていったかいがあるわ。

ありがとうございました。
じゃあこのへんで…

ちょまてや。
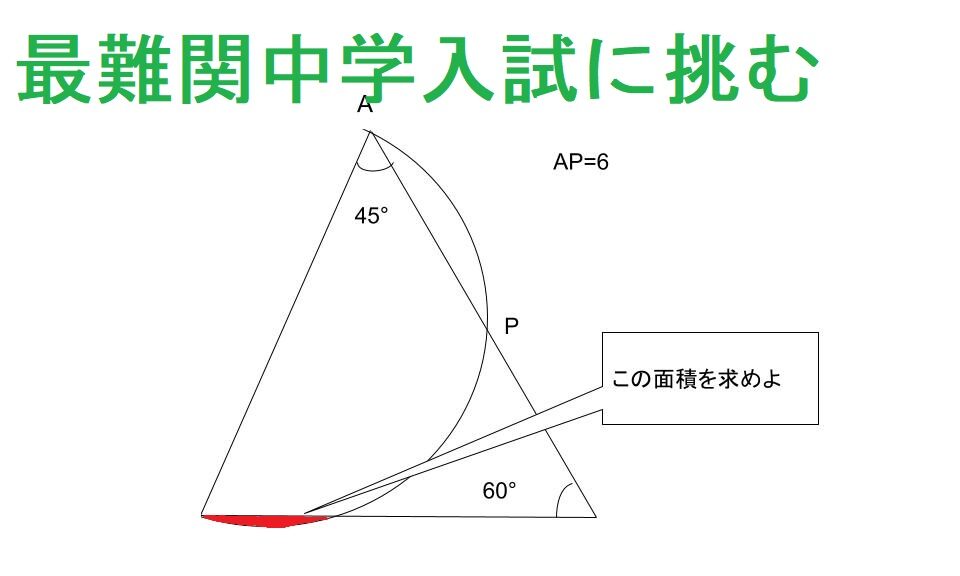
これからやで本番は。
一刻も早く帰りたいまもる。
果たして問題は解けるのであろうか。

後半に続く。


コメント