今日はカンガルー君が、
新たに問題を見つけたから、
解説するということで、
カンガルーハウスに今日も来ました。

こんにちはカンガルー君。
今日も図形の勉強かい?

おーまもるやないか。
今日も中学入試をやるでー。

僕はもう二十歳を超えましたよ。

頭脳は小学3年生やろ。
今日の問題はこちら。
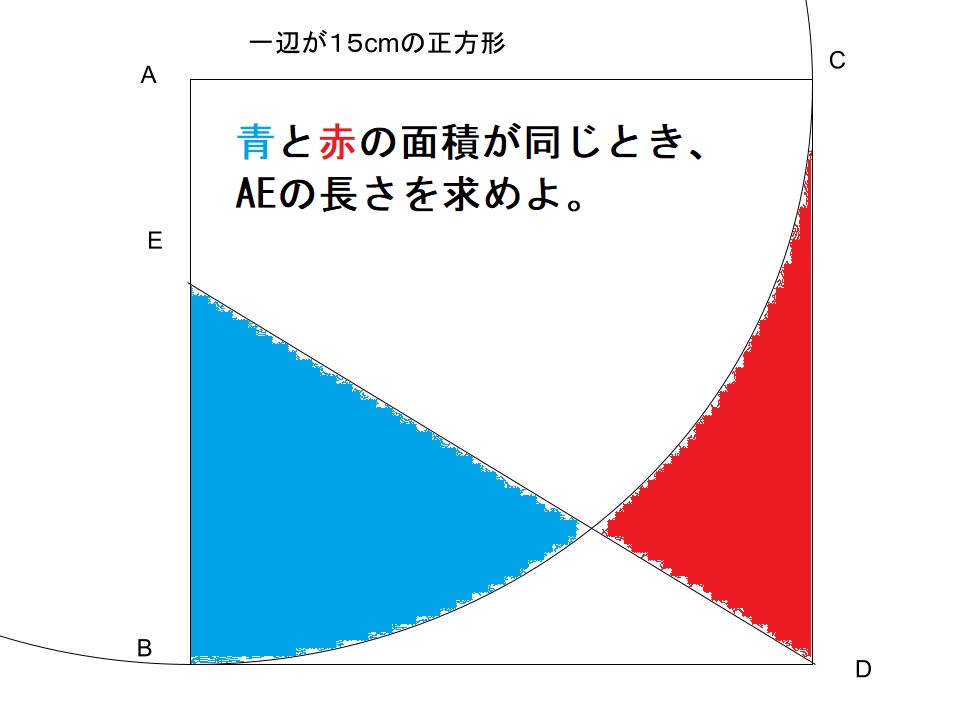

ひえー!
これはまた、難題ですね。

これもちょっと見方を変えれば、
すぐに解けるんやで。

その、見方を変えたりが、
難しいじゃないか。

頭の体操や。
視点を変えるっちゅうのは、
いろんな場面で役に立つんやで。

そうなんですか。
じゃあ解説お願いいたします。

まず考えることは、
青と赤の面積が同じということは、
どうゆうことや?

青と赤の面積が同じということは、
青と赤の面積が同じということだね。

そうゆうことや!
ってアホか。
2回言うてるだけやん。

えへへ。

つまりは、この正方形を半径とした、
おうぎ形と、台形のAEDCの面積が、
同じなんや。
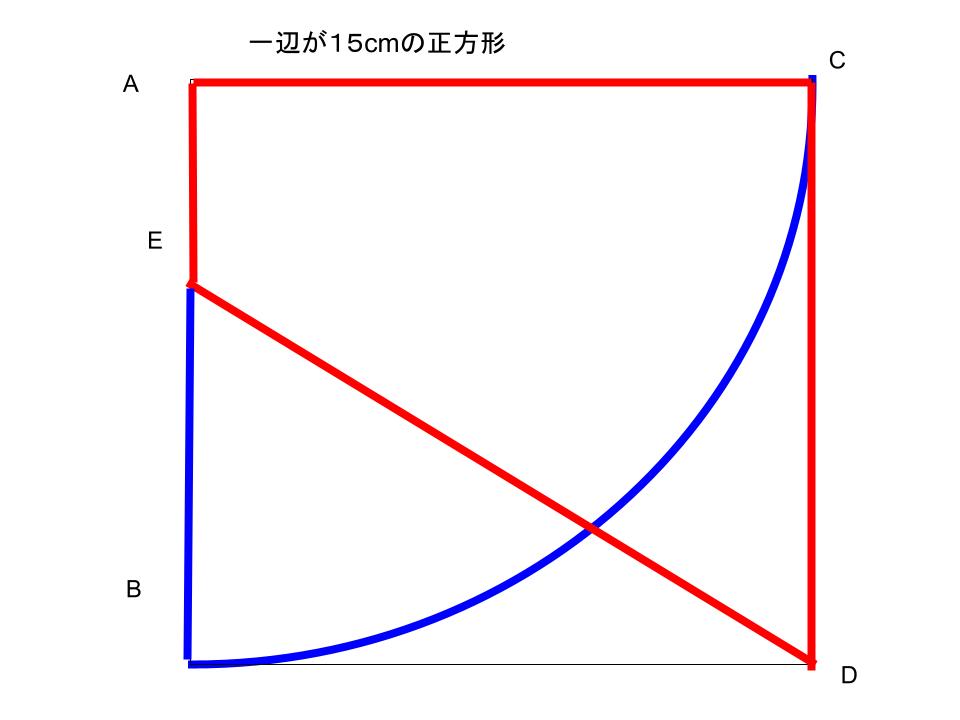

なるのどね。
このおうぎ形の面積は求められるね。

求めてみいや。

15x15x3.14÷4=176.625

電卓叩いたやろ?
まぁええわ。

あとは台形の面積だね。
でも、AEが求められないから、
結局出せないよ。

ほんましょうもない。
おうぎ形の面積が出たなら、
もう答えみたいなもんやろ?

どうゆう意味ですか?

台形の求め方は?

(上底+下底)×高さ÷2

せや、つまりは、
(AE+15)×15÷2=176.625

一次方程式ですね。

176.625を2倍すると、
353.25やろ。

…そうですね。

353.25を15で割ると、23.55や。

…はぁ、

23.55から15を引けば8.55

つまりは、AEが8.55cmのとき
てことだね。

どうや?いい勉強になったやろ。

そうだね。
おうぎ形と台形の面積が、
同じって考えることが大事なんですね。

そうゆうことや!
共通する図面を探して、
これとこれが同じだから、
これとこれが同じなんだと、
見つけることが大事…

ああ、もうこんな時間だ、
じゃあ今日はこの辺で帰るよ。
さようなら。

気を付けて帰りやー。
足早にカンガルーハウスを立ち去るまもるであった。


コメント