カンガルー君が円周率が3.05より大きい事を証明してやるって言うもんで、
カンガルー君の家にわざわざやってきたまもる。
前回の説明で円周率が3より大きい事、
4より小さいことを見事証明して見せたカンガルー君。
果たして3.05より大きい事を証明できるか。

さて、カンガルー君。
ここからが正念場だよ。

正六角形では足りへんねん。
次は正12角形や。

せせ、正12角形!!
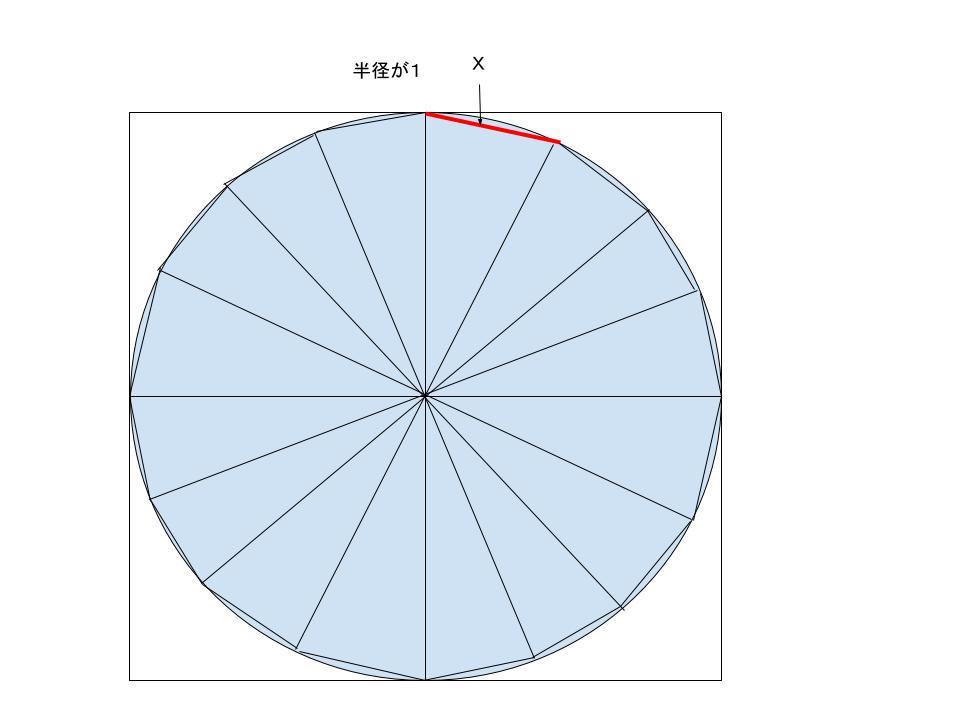

正12角形を12等分した、
このXの長さが分かればええねん。

Xの長さが分かるとなんで、証明できるのさ。

円周が3.05より大きい事を証明すんのやから、
直径が2で円周が6.1になるやろ、
Xの長さ×12が6.1より大きければ、
その外側を通る円周はそれよりも大きいということや。

Xの長さが肝なんだね。
で、そうやって求めるのさ。

余弦定理や。

よよよ、余弦定理!!!

この三角形の角度はいくつや?

360度を12で割るから30度。

やるやないかい。
30度の三角形の2辺が1の
もう一つの辺を求めるのやから、

ふむふむ。

Xの二乗=1の二乗+1の二乗-2cosine30°

もうわけかなんねー。

cosine30°は2分の√3や。

あー、はいはい。

X=√2-√3
√3は2重根号やから、
2重根号をはずすんや。

なるほどね、2重根号ね。
あー懐かしいですね。

X=(√3-1)÷√2になるわけや。

はいはい。

√3は人並みにおごれや。
√2は人世人世にひとみごろや。

それはなんか聞いたことある。

計算上のXを低めに設定する為、
分母√2を1.415、
分子の√3を1.734とする。

√2が1.4142、
√3が1.7340だからね。

X=0.51
少数第三位切り捨てや。

つまり12Xは12×0.51ということで。

6.12や。

すすすごい。
これがカンガルー君の実力なのか。

12角形の周りの辺の長さは6.1より大きい。
つまりは円周率は3.05より大きいねん。

すごいよカンガルー君。
途中何言ってるか分からなかったけど、
最高だよ。

まもる分かってくれたか。
これがカンガルー魂や。

じゃあ僕はこれで

気つけてかえりやー。
カンガルー君を後にするまもるは。
あの伝説の数式フェルマーの最終定理について、
挑むことになるとは。
この時はまだ知ることもなかった。



コメント