今日はカンガルー君が、ヒポクラテスの三日月が解けたから、
教えたるゆうことで、
カンガルー君の家にやって参りました。

こんにちはカンガルー君。
今日はヒポクラテスの三日月を
教えてくれるんだって?

せや、ヒポクラテスの三日月や。
聞いたことくらいあるやろ?

いや、聞いたことないよ。
ジブリの新作か何かですか?

ちゃうわボケ❕
中学入試の算数や。

算数くらい僕だって解けるよ。
だてに高校は卒業してないからね。

なめとんな。
じゃあこの問題を解いてみ
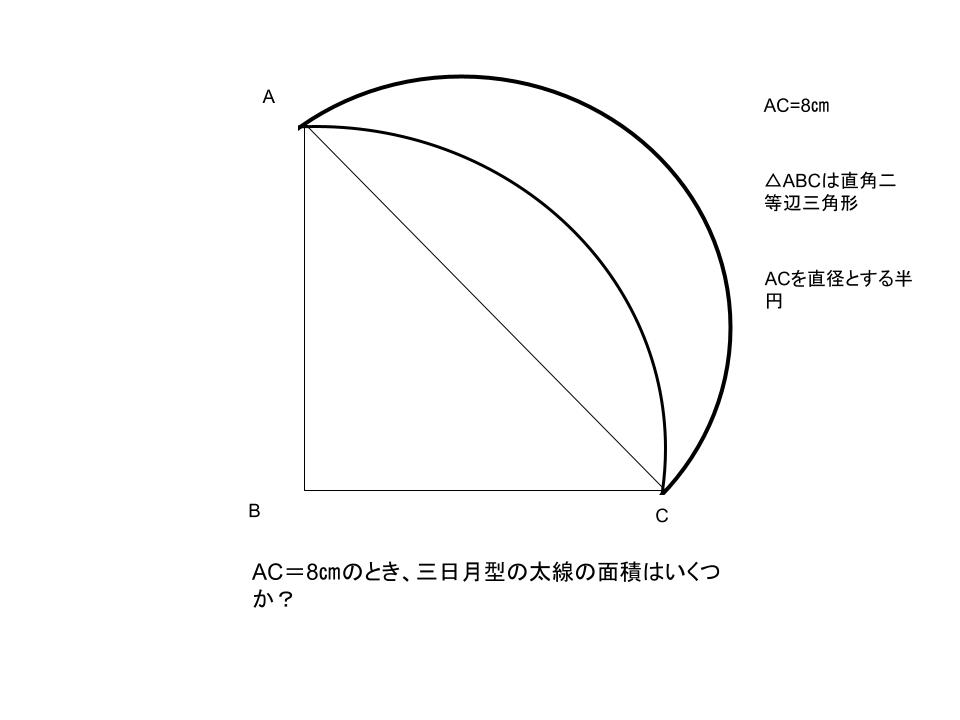

これが中学入試ですか?
問題の内容すら意味不明だよ。

中学入試やから当然√は使えへん。
さあ答えてみいや。
高校卒業したんやろ?

まま、まいったよカンガルー君。
教えておくれよ。

ちっ、しょうもない。
教えてやるから耳かっぽじって、
よく聞きやがれ!

段々と口調が悪くなっていっているよ、
カンガルー君。

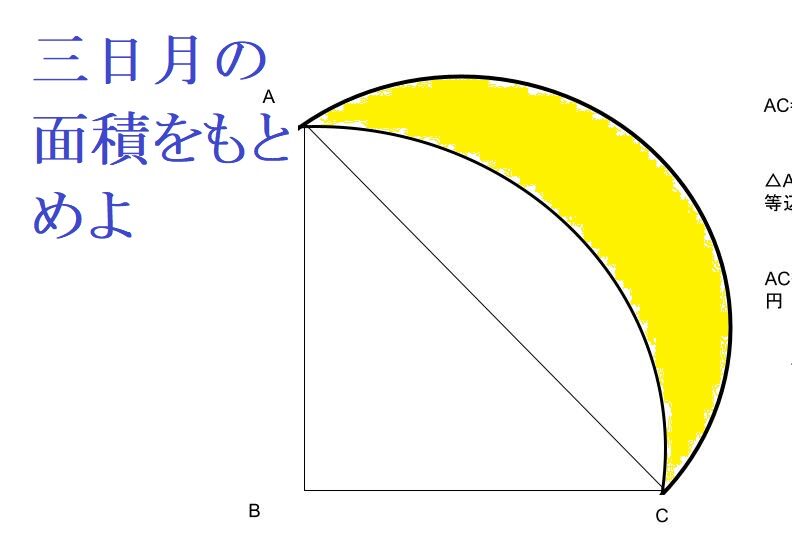
あの三日月型の面積をもとめるには、
三角形+ACを直径とする半径-
おうぎ形の面積や。

ほうほう。

まずは三角形の面積からいこか。

斜めの辺しか長さが分からないから、
もとめられないよ。

ホンマあほやな。
直角二等辺三角形は、
二つ重ねると何になる。

正方形?

せや、やるやないかい。
正方形になるんや。
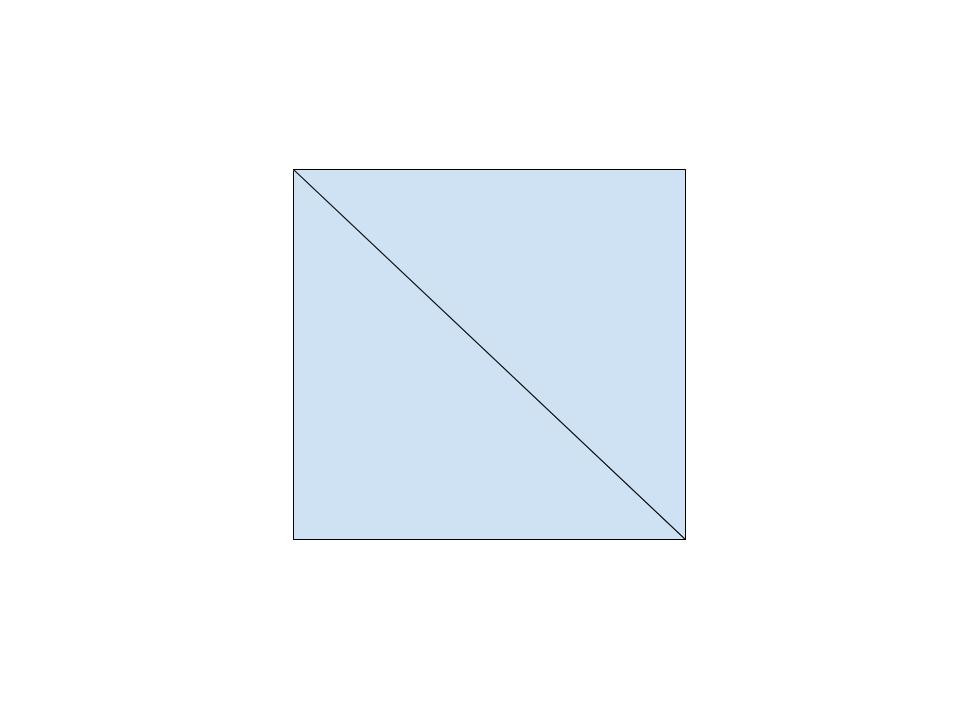

それで?正方形になったからって、
面積わからないじゃないか。

ほんま学がない奴は、
嫌いやわ。
正方形はひし形の仲間やろ、
ひし形の面積の求め方は?

確か対角線×対角線÷2

ほんまにスッキリや。
感動したで。

それくらい分かりますよ。

さらに÷2をすれば、
三角形の面積が出るんや。

ということは、対角線が8㎝だから、
8×8÷2÷2ということは、
16だ。

正解や!半円の面積は簡単やろ?

半径×半径×3.14÷2だから、
4×4×3.14÷2で、
えーと、

ここは、8×3.14ということに、
しとこうや。

最後まで計算しないんだね。

ほいで、残りはおうぎ形の面積や。
直角二等辺三角形に対するおうぎ形やから、
半径×半径×3.14÷4で求められるわけや。

でも、ABの長さが分からないよ。

このおうぎ形の面積をもとめるのが、
今回の最大の試練や。

ABの長さが分からないのに、
求められるのかい?

わてに不可能はない。
果たしてまもるは、無事にカンガルー君の家から帰れるのだろうか。
後半に続く。


コメント