今日はカンガルー君が、
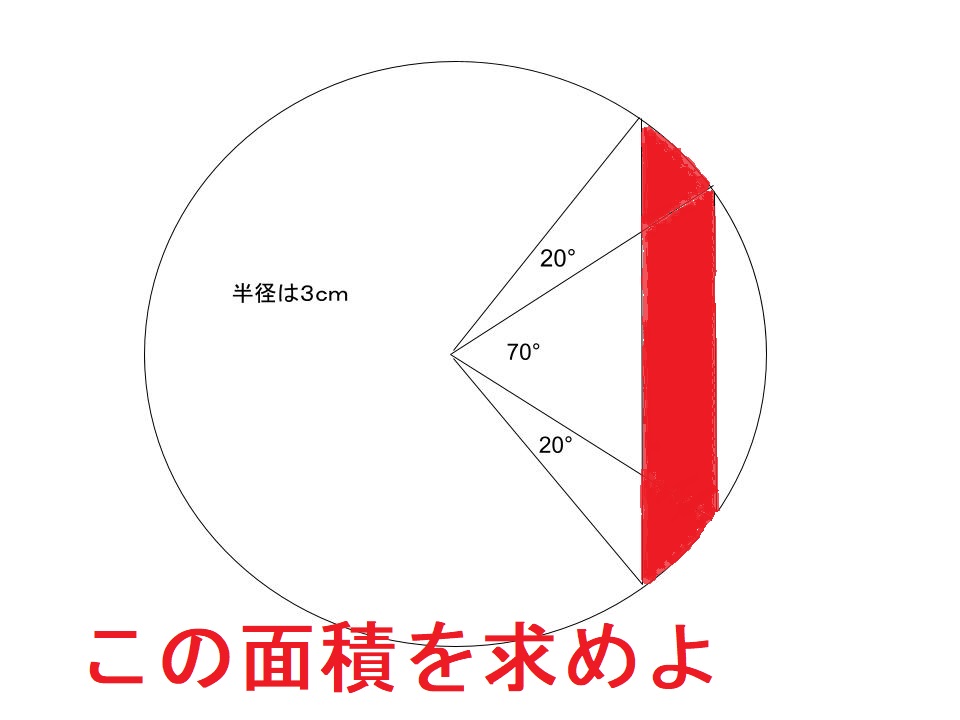
この円の赤い部分の面積を求めるから、
ちょっと来てほしい言うことで、
雨の中歩いてきました。

まもる
こんにちはカンガルー君。
雨がすごいね今日は。

カンガルー君
もう夏も終わりやな。
今日は赤部分の面積を求めるぜよ。

まもる
図形が好きだねカンガルー君。

カンガルー君
どうやって求めると思う?

まもる
見当が付きません。

カンガルー君
せやろ。これも小学生が解く
中学入試やで。

まもる
今の小学生はすごいなあ。

カンガルー君
ちょっと頭をひねれば、
解ける問題なんやで。

まもる
頭をひねろうがねじろうが
僕には解けないよ。

カンガルー君
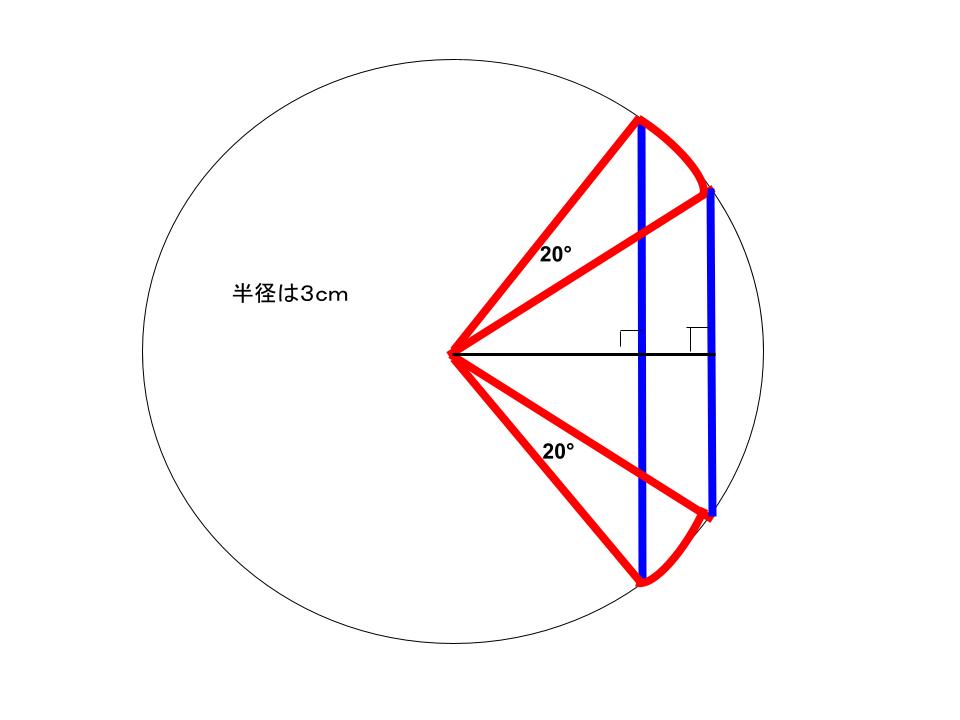
まずは、一本線を引くんや
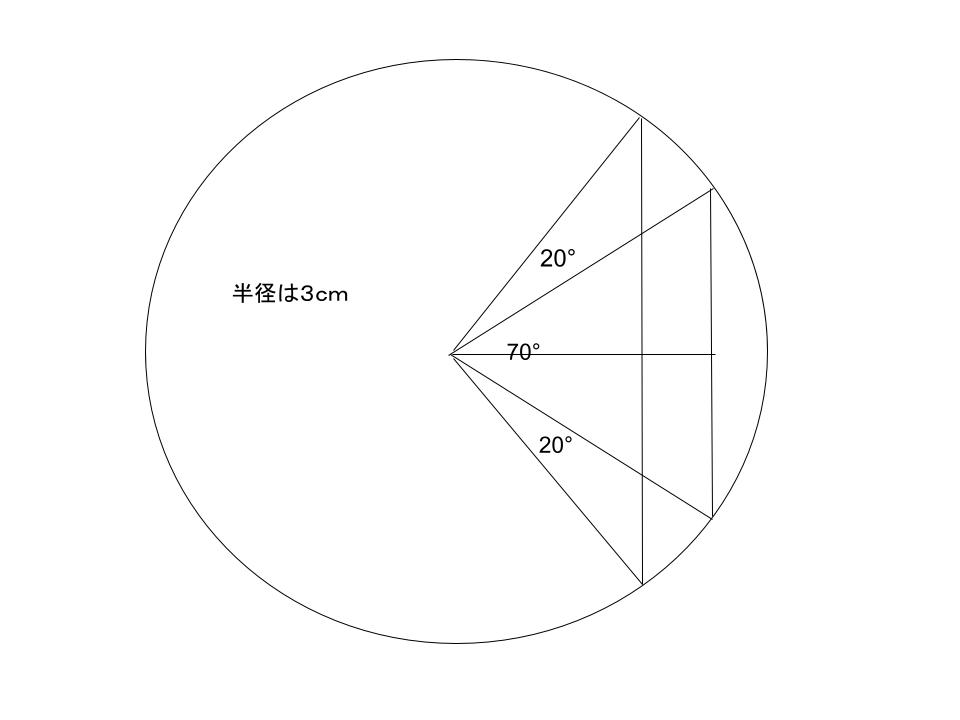

まもる
70°の三角形を
二同分するんだね。

カンガルー君
すると35°の直角三角形が
できるんや。

まもる
そうですね。
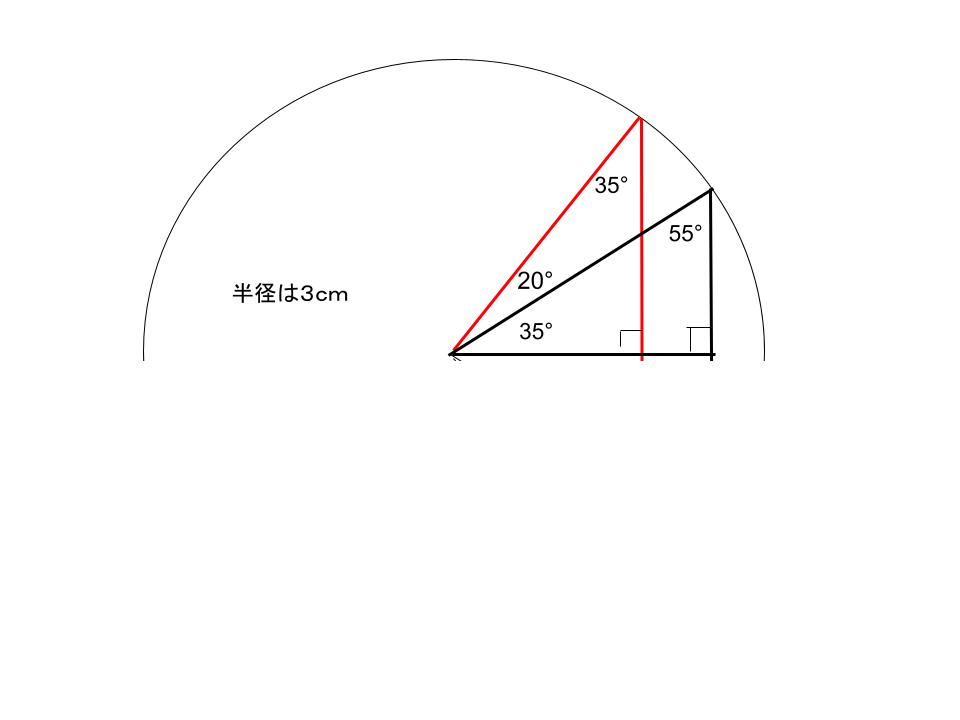

カンガルー君
すると、この黒三角形と、
赤三角形の角度が全部一緒や。

まもる
確かに55°、35°、90°の
直角三角形だね。

カンガルー君
そして、半径が3cmやから、
全ての辺の長さも一緒や。

まもる
つまり、この三角形二つは、
同じ三角形ということだね。
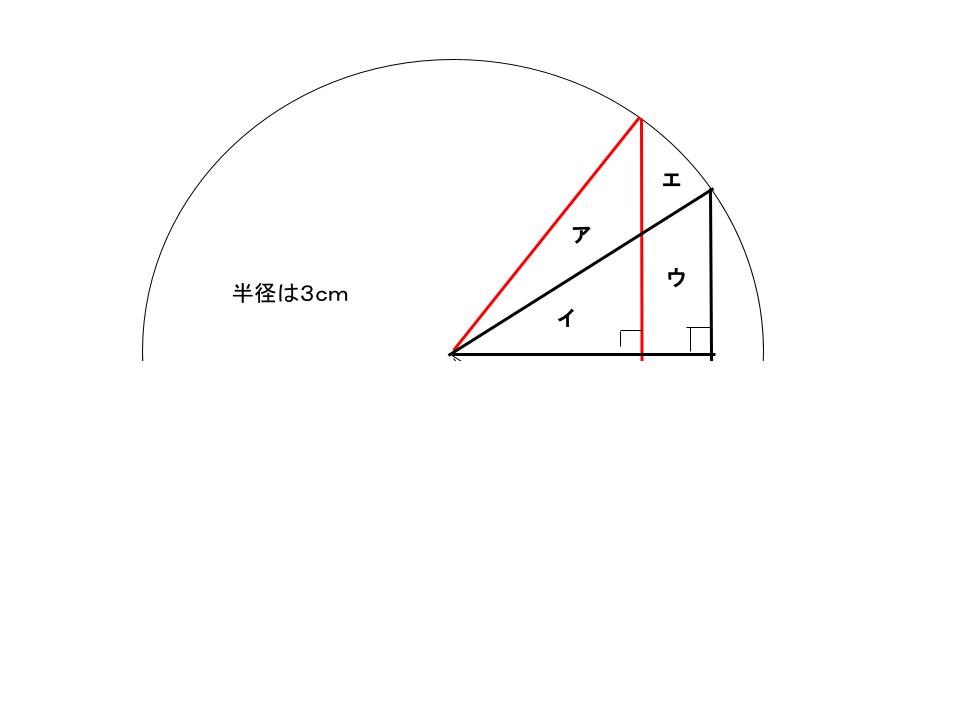

カンガルー君
求めたいのは、ウとエの部分や。
これを2倍にしたのが答えや。

まもる
そうなりますね。

カンガルー君
ア、イの三角形と、
イ、ウの三角形は、
一緒やろ。

まもる
はぁ、

カンガルー君
つまりは、アとウは同じ面積やねん。

まもる
おおー。すごいなあ。

カンガルー君
つまりは、アとエは、
ウとエやねん。

まもる
ちょっと何言ってるか、
わからないけど。

カンガルー君
つまりは、赤いおうぎ形の面積は、
青いの面積と同じやねん。
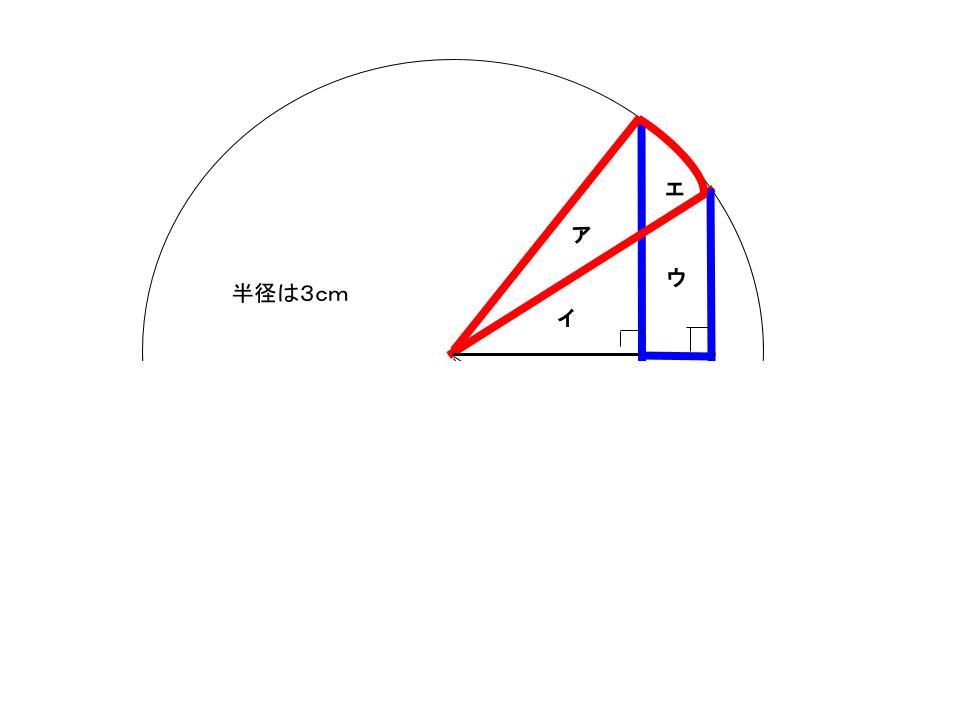

まもる
それは分かりやすいね。

カンガルー君
つまりは、この20°のおうぎ形二つが、
求める面積の答えやねん。

まもる
ということは、
3×3×3.14×(40÷360)
だね。

カンガルー君
すると答えは?

まもる
3.14だ…

カンガルー君
どや?

まもる
すごい、すごいよカンガルー君。
こんな求め方が有るなんて、
感動したよ。

カンガルー君
似たような形のものを、
探せば自ずと答えは導かれるねん。

まもる
じゃあ、帰るよ。

カンガルー君
気を付けて帰りやー。
九月の上旬なのにすっかり寒くなってきた道を、
雨の中歩きながら帰るまもるは、
半袖で来るんじゃなかったと、
後悔するのでった。


コメント